Source: CurveCompression.zip

Project Objective: To experiment on the compression and decompression of polygonal curves and using hausdorff distance to measure similarities between curves.

List of Modules

 

Modules	Explanation
Normalization	Express curve vertex coordinates in the range of zero to one.
Quantization	Convert real coordinates in the range of zero to one to integer coordinates in the range of 0 to 2^b, where b is the number of bits given by the user (default 10)
Prediction	Given vertices v(i), v(i+1), v(i+2), this function computes the integer coordinates for v(i+3) using the quadratic predictor: v(i+3) = v(i) + 3[v(i+2) - v(i+1)].  It then computes the residuals: the difference vector between the prediction and the actual coordinates.
Statistics	Display compression statistics
Compression	Compute the Huffman tree and codes for the residuals. Encode the codebook using binary tree. Encode the residuals.
Decompression	Read the compressed file and reconstruct the Huffman tree. Decode the residuals and use them with the information contained in the header to computer the actual quantized curve.
Dequantization	Converts the integer coordinates back to its real coordinates from zero to one
Denormalization	Convert the coordinates in the range from zero to one to original curve coordinates (with the min-max box obtained from the header)
Subdivision	Subdivide the current curve using either B-spline, 4-point, or Jarek's subdivision method
Simplification	Simplify the curve by using B-bit quantization and removing all vertices that are identical to their previous neighbor.
Hausdorff	To compute the Hausdorff distance between two curves.  Sample one curve, then compare the distances between vertices on this curve against edges on the other.  The switch the curves.

 

Link to the source code: Curve doc, Compression doc
Language:C++
System: Windows, Visual Studio 6.0

Sources of inspiration:

• Bit file access, Adaptive Huffman Codeing http://ourworld.compuserve.com/homepages/marktoml/cppstuff.htm

Description of binary format: 

header:

201 0.000000 -0.999965 10.000000 1.000000 10 10 0 0 1024 5 1023 10 1021 396 7 17

# of vertices in the curve min X, min Y coordinates max X, max Y coordinates # of bits X, # of bits Y compression scheme (0 for huffman) vertex 0 x, y vertex 1 x, y vertex 2 x, y # of data points to compress # of symbols appeared # of bits used to encode the huffman binary tree

 

How's the header encoded?
The header is compressed using the adaptive huffman encoding on normal ASCII character set

How's the codebook encoded?
The vocabulary of the code book is included in the header and compressed using the adaptive huffman encoding on ASCII character set. The structure of the codebook is encoded as a huffman binary tree (traversed in depth first order)

Codec

• Input: A link to the input file in ASCII format, which contains the number of points in the first line and then two coordinates in [0, 1023] per line.
• Compressed: A link to the compressed binary file using 10-bit quantization
• B: corresponding half-diagonal error bound
• N: # of vertices
• L: Average edge length L
• F: Total size F in bits of the compressed file
• H%: proportion in % of the file size used for the header
• E: Entropy E
• Excess: (F-NE)/(NE)
• HD: The Hausdorff error between the original and the simplified curve
• HDB: The Hausdorff error between the original and the curve obtained by B-Spline subdivision of the simplified curve
• HD4: The Hausdorff error between the original and the curve obtained by 4-point subdivision of the simplified curve
• HDJ: The Hausdorff error between the original and the curve obtained by Jarek subdivision of the simplified curve

	picture	input	compressed	B	N	L	log2(L)	F	F/N	H%	E	excess
1		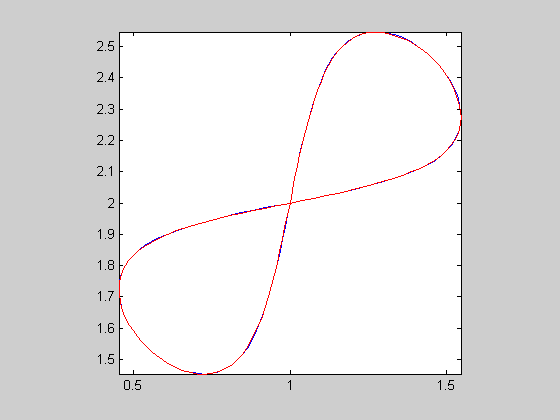c1	c1c	0.000753754	128	0.0267676	-5.22337	1096	8.5625	42.3358	2.2051	2.88305
2		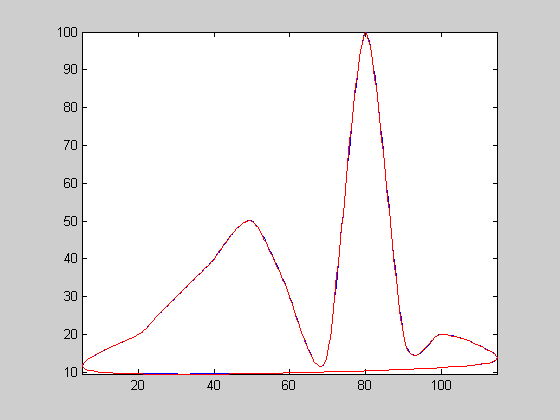c2	c2c	0.0693933	352	1.17983	0.238581	2152	6.11364	22.3048	2.21755	1.75694
3		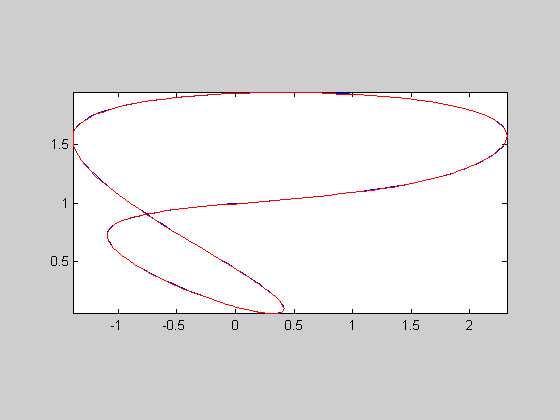c3	c3c	0.00202932	192	0.0604328	-4.04852	1432	7.45833	34.0782	2.23943	2.33046
4		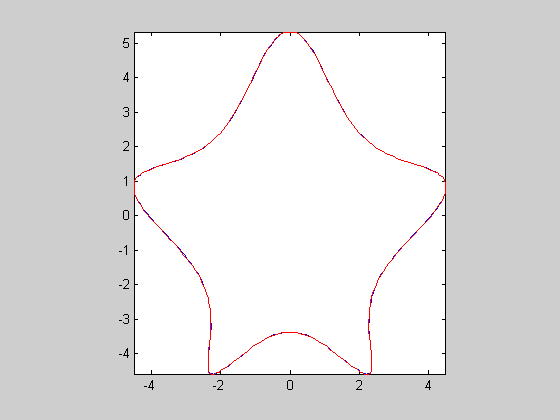c4	c4c	0.00654761	320	0.0969711	-3.3663	2200	6.875	23.2727	2.49895	1.75115
5		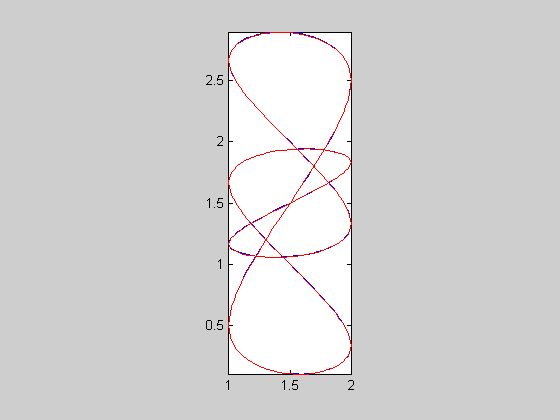c5	c5c	0.00145135	256	0.0459533	-4.44369	1824	7.125	24.5614	2.5419	1.80303

Simplification and Error

curve 2:

bits	picture	input	compressed	B	N	L	log2(L)	F	F/N	H%	E	excess	HD	HDB	HD4	HDJ
5		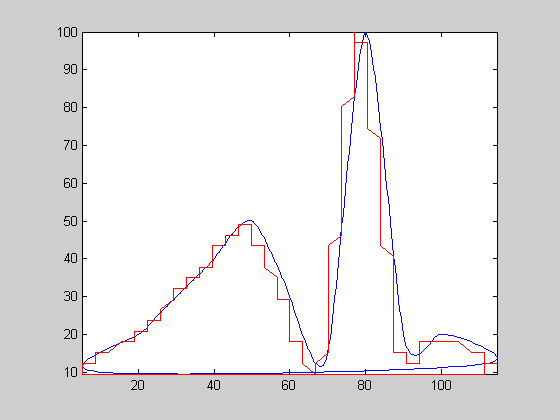c2	c25sc	0.0693933	147	3.21423	1.68447	1128	7.67347	42.5532	1.9546	2.92586	3.96537	3.33859	4.01511	3.75644
6		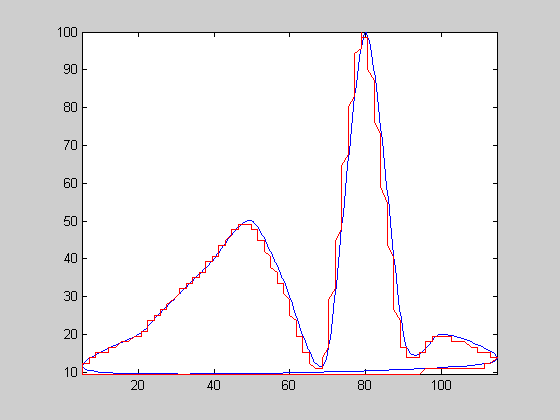	c26sc	0.0693933	212	2.17404	1.12038	1552	7.32075	30.4124	2.28518	2.20358	1.86811	1.58166	1.89999	1.78198
7		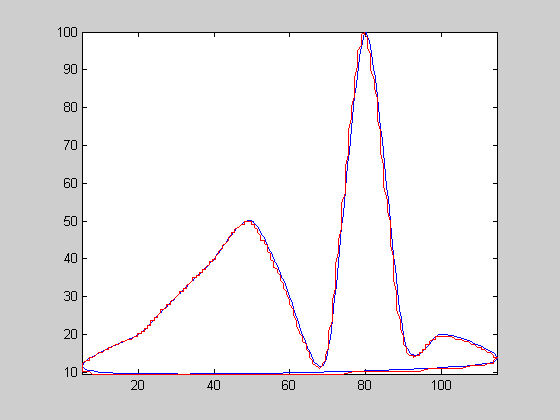	c27sc	0.0693933	289	1.53073	0.614219	2008	6.9481	23.9044	2.36244	1.94107	1.03516	0.88165	1.04669	0.983156
8		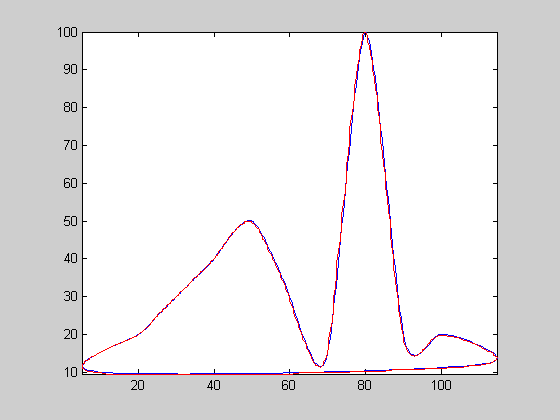	c28sc	0.0693933	338	1.25048	0.322486	1976	5.84615	23.4818	2.08257	1.80719	0.493794	0.412394	0.493794	0.449386
9		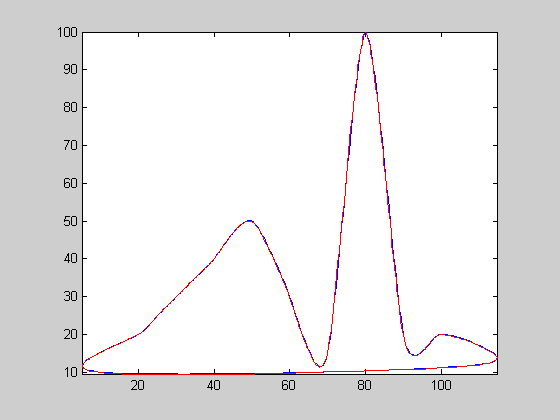	c29sc	0.0693933	352	1.18568	0.245719	2288	6.5	20.6294	2.37361	1.73844	0.258593	0.245064	0.258593	0.252683

curve 4:

bits	picture	input	compressed	B	N	L	log2(L)	F	F/N	H%	E	excess	HD	HDB	HD4	HDJ
5		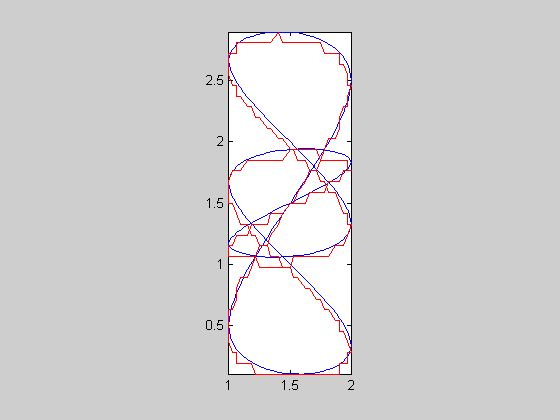c5	c55sc	0.00145135	222	0.0612834	-4.02836	1664	7.4955	27.8846	2.41251	2.10692	0.0872673	0.0851447	0.0932807	0.0909566
6		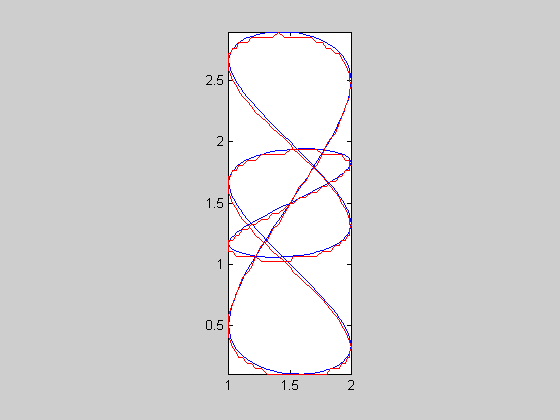	c56sc	0.00145135	251	0.0493258	-4.34151	1760	7.01195	26.8182	2.31831	2.0246	0.0433849	0.0413729	0.0457512	0.0445049
7		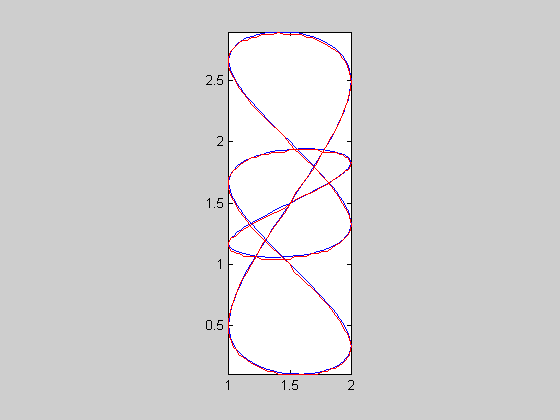	c57sc	0.00145135	255	0.0466396	-4.4223	1736	6.80784	27.1889	2.22666	2.05742	0.0215582	0.0197974	0.0224055	0.0216482
8		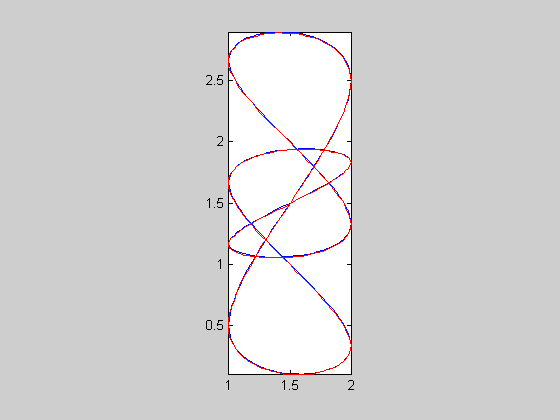	c58sc	0.00145135	256	0.046108	-4.43884	1760	6.875	25.9091	2.40525	1.85833	0.0106448	0.00957395	0.0107327	0.0103482
9		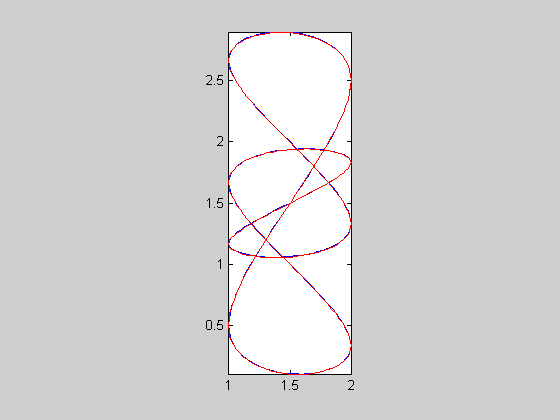	c59sc	0.00145135	256	0.0460165	-4.4417	1928	7.53125	23.2365	2.72464	1.76412	0.005605	0.00563043	0.005605	0.00556266

paper link